README.md

Tries Data-Structures and Algorithms

01. Implement Trie (Prefix Tree)

Leetcode Problem URL

A trie (pronounced as "try") or prefix tree is a tree data structure used to efficiently store and retrieve keys in a dataset of strings. There are various applications of this data structure, such as autocomplete and spellchecker.

Implement the Trie class:

• Trie() Initializes the trie object.
• def insert(word: str) Inserts the string word into the trie.
• def search(word: str) -> bool Returns true if the string word is in the trie (i.e., was inserted before), and false otherwise.
• def startsWith(prefix: str) -> bool Returns true if there is a previously inserted string word that has the prefix prefix, and false otherwise.

Example 1:

Input
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
Output
[null, null, true, false, true, null, true]

Explanation
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // return True
trie.search("app");     // return False
trie.startsWith("app"); // return True
trie.insert("app");
trie.search("app");     // return True

obj = Trie()
word1 = 'apple'
obj.insert(word1)
print(obj.search(word1)) # True
word2 = 'app'
print(obj.search(word2)) # False because the word "app" is not present in the Trie object
prefix = 'app'
print(obj.startsWith(prefix)) # True because the previously inserted string `word` has the prefix `prefix`
obj.insert(word2)
print(obj.search(word2)) # True because the word "app" has been inserted in the Trie object

Explanation

TrieNode Class

The TrieNode class represents each node in the Trie. Each node contains:

• A dictionary children to store the children nodes.
• A boolean endOfWord to indicate if the node marks the end of a word.

Trie Class

The Trie class manages the TrieNode and implements the three methods insert, search, and startsWith.

1. Initialization

class Trie:
    def __init__(self):
        self.root = TrieNode()

2. Insert Method

The insert method adds a word to the Trie. Starting from the root, it iterates through each character in the word. If a character is not already a child of the current node, it creates a new TrieNode. After processing all characters, it marks the last node's endOfWord as True.

3. Search Method

The search method checks if a word is in the Trie. Starting from the root, it iterates through each character in the word. If a character is not found in the current node's children, it returns False. If all characters are found, it returns True only if the last node's endOfWord is True.

4. StartsWith Method

The startsWith method checks if there is any word in the Trie that starts with the given prefix. It follows a similar process to the search method but returns True as soon as all characters in the prefix are found.

Efficiency Analysis

• Insert Method:

  • Time Complexity: $(O(n))$, where $(n)$ is the length of the word. This is because each character of the word is processed once.
  • Space Complexity: $(O(n))$ in the worst case, where each character in the word requires a new TrieNode.

• Search Method:

  • Time Complexity: $(O(n))$, where $(n)$ is the length of the word. Each character is checked once.
  • Space Complexity: $(O(1))$, as no additional space is needed beyond the input word.

• StartsWith Method:

  • Time Complexity: $(O(m))$, where $(m)$ is the length of the prefix. Each character in the prefix is checked once.
  • Space Complexity: $(O(1))$, similar to the search method.

Explanation

1. Insertion of "apple":

   • Traverse through each character in "apple" and create new TrieNode for each character.
   • Mark the last node (representing 'e') with endOfWord = True.

2. Search for "apple":

   • Traverse through each character in "apple".
   • Since all characters are found and the last node has endOfWord = True, return True.

3. Search for "app":

   • Traverse through each character in "app".
   • The last node (representing 'p') does not have endOfWord = True, so return False.

4. StartsWith "app":

   • Traverse through each character in "app".
   • Since all characters are found, return True.

5. Insertion of "app":

   • Traverse through each character in "app" and use existing nodes.
   • Mark the last node (representing 'p') with endOfWord = True.

6. Search for "app" again:

   • Traverse through each character in "app".
   • Since all characters are found and the last node has endOfWord = True, return True.

---

---

02. Design Add and Search Words Data Structure

Leetcode Problem URL

Design a data structure that supports adding new words and finding if a string matches any previously added string.

Implement the WordDictionary class:

• WordDictionary() Initializes the object.
• void addWord(word) Adds word to the data structure, it can be matched later.
• bool search(word) Returns true if there is any string in the data structure that matches word or false otherwise. word may contain dots '.' where dots can be matched with any letter.

Example 1:

Input
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
Output
[null,null,null,null,false,true,true,true]

Explanation
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b.."); // return True

obj = WordDictionary()
word1 = 'bad'
word2 = 'dad'
word3 = 'mad'
obj.addWord(word1)
obj.addWord(word2)
obj.addWord(word3)
print(obj.search("pad")) # False because "pad" is not present in the Trie object
print(obj.search(".ad")) # True because ".ad" matches "bad", "dad", or "mad"
print(obj.search("b..")) # True because "b.." matches "bad"

Explanation

TrieNode Class

The TrieNode class represents each node in the Trie. Each node contains:

• A dictionary children to store the children nodes.
• A boolean endOfWord to indicate if the node marks the end of a word.

WordDictionary Class

The WordDictionary class manages the TrieNode and implements the methods addWord and search.

1. Initialization

class WordDictionary:
    def __init__(self):
        self.root = TrieNode()

2. AddWord Method

The addWord method adds a word to the Trie. Starting from the root, it iterates through each character in the word. If a character is not already a child of the current node, it creates a new TrieNode. After processing all characters, it marks the last node's endOfWord as True.

3. Search Method

The search method checks if a word is in the Trie. It uses a Depth-First Search (DFS) to handle the dots '.'.

The dfs function is a helper function for recursive DFS:

• It takes the current index j and the current node root.
• For each character in the word starting from j:
  • If the character is a dot '.', it recursively checks all children nodes.
  • If the character is not a dot, it checks if the character exists in the current node's children.
• The function returns True if it successfully matches all characters and the last node marks the end of a word.

Efficiency Analysis

• AddWord Method:

  • Time Complexity: $(O(n))$, where $(n)$ is the length of the word. Each character of the word is processed once.
  • Space Complexity: $(O(n))$ in the worst case, where each character in the word requires a new TrieNode.

• Search Method:

  • Time Complexity: In the worst case, it can be $(O(m \times 26^m))$, where $(m)$ is the length of the word. This is because for each dot '.', it may need to check all possible 26 child nodes, resulting in a combinatorial explosion.
  • Space Complexity: $(O(m))$ for the recursion stack in the worst case where $(m)$ is the length of the word.

---

---

03. Word Search II

Leetcode Problem URL

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

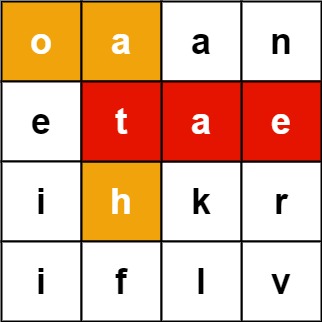
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

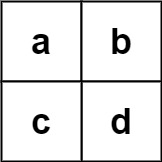
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

obj = Solution()

board1 = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]
words1 = ["oath","pea","eat","rain"]
res1 = obj.findWords(board=board1, words=words1)
print(res1)

board2 = [["a","b"],["c","d"]]
word2 = ["abcb"]
res2 = obj.findWords(board=board2, words=word2)
print(res2)

Explanation

To solve this problem, we utilize a combination of a Trie (prefix tree) and Depth-First Search (DFS). The Trie helps efficiently check if the prefixes of the words are present while performing the DFS.

TrieNode Class

The TrieNode class represents each node in the Trie. Each node contains:

• A dictionary children to store the children nodes.
• A boolean endOfWord to indicate if the node marks the end of a word.
• An integer refs to keep track of the number of references to this node, which helps with optimization during word removal.

Solution Class

The Solution class manages the Trie and implements the findWords method to find all valid words on the board.

1. Initialization

The Solution class initializes the root of the Trie.

class Solution:
    def __init__(self) -> None:
        self.root = TrieNode()

2. FindWords Method

The findWords method populates the Trie with the given words and uses DFS to find all valid words on the board.

• Adding Words to Trie

def findWords(self, board: list[list[str]], words: list[str]) -> list[str]:
    root = self.root
    for w in words:
        root.addWord(w)

• DFS Method

The dfs function performs the Depth-First Search on the board to find all valid words. It:

• Checks boundary conditions and if the current cell has already been visited or is not in the Trie.

• Adds the cell to the visited set.

• Checks if the current node marks the end of a word. If yes, it adds the word to the result set and removes it from the Trie.

• Recursively explores all four possible directions (up, down, left, right).

• Removes the cell from the visited set.

• Iterate Through Board

Finally, the method iterates through each cell in the board and initiates a DFS from that cell.

---

---

Efficiency Analysis

• Adding Words to Trie

  • Time Complexity: $(O(N \cdot M))$, where $(N)$ is the number of words and $(M)$ is the maximum length of a word. Each character of each word is processed once.
  • Space Complexity: $(O(N \cdot M))$, where $(N)$ is the number of words and $(M)$ is the maximum length of a word. This is the space required to store the Trie.

• DFS Search

  • Time Complexity: $(O(m \cdot n \cdot 4^L))$, where $(m)$ and $(n)$ are the dimensions of the board and $(L)$ is the maximum length of a word. Each cell initiates a DFS that explores all possible directions.
  • Space Complexity: $(O(L))$, where $(L)$ is the maximum length of a word. This is the space required for the recursion stack during DFS.

---

---