闫令琪 Games 101-现代计算机图形学入门作业

课程链接: https://www.bilibili.com/video/BV1X7411F744/

task0

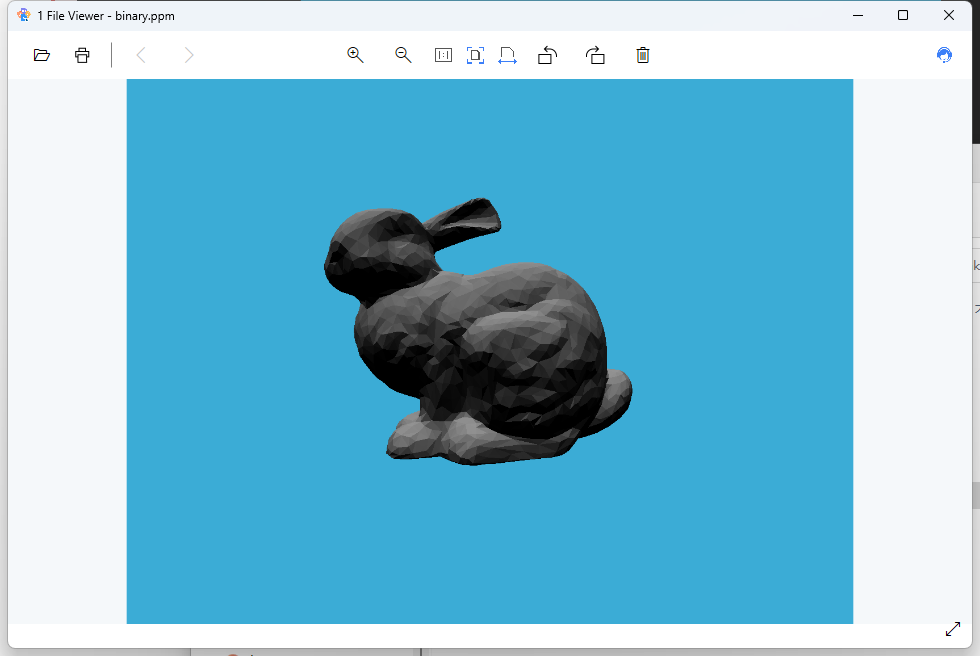
略

task1

旋转

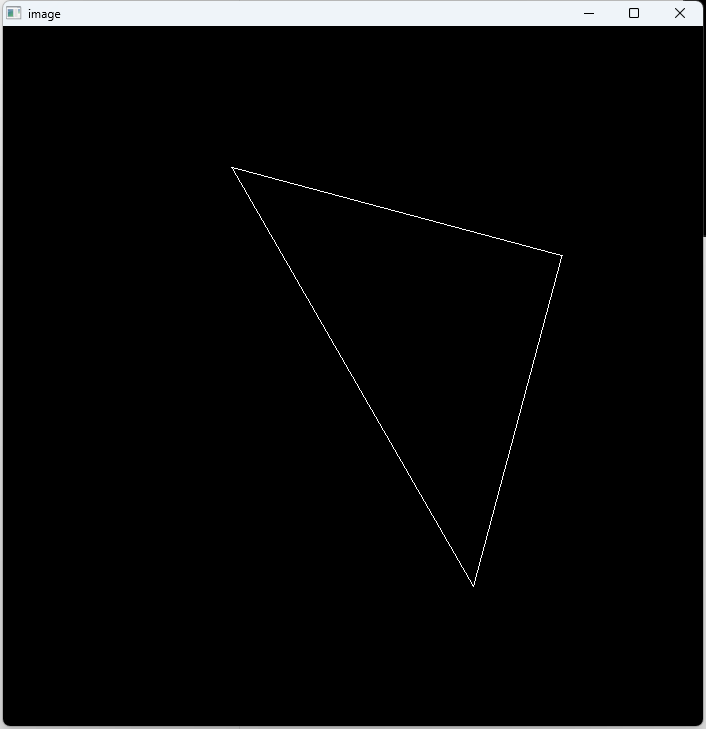
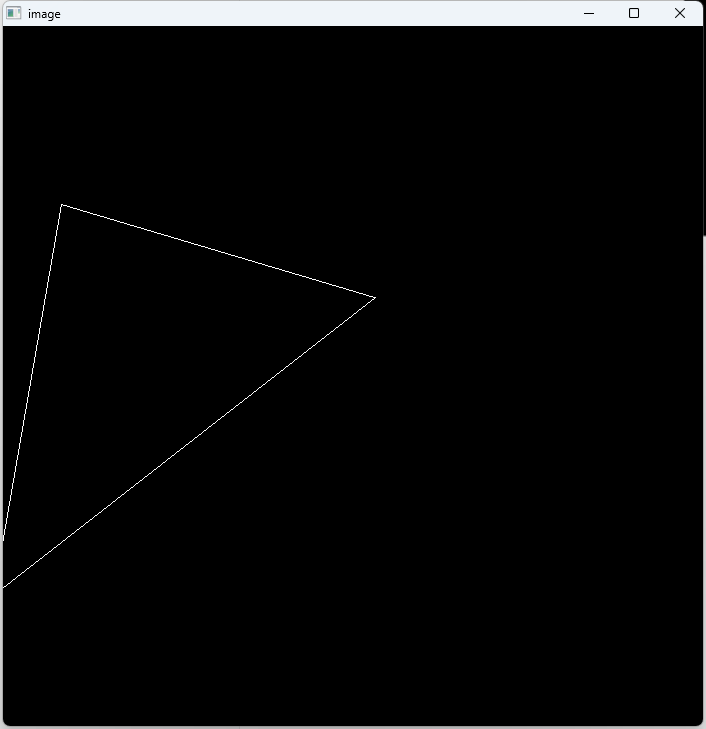
绕任意轴旋转(0, 0, 1), 注意旋转角度不能过大，否则三角形超出屏幕外frame_buf会越界

task2

2*2 Super Sampling Anti-Aliasing

task3

Normal模型

• BaryCentric Coordinates Interpolation

Blinn-Phong模型

• 计算光照 Specular, Diffuse, Ambient

Blinn-Phong模型 + Texture

• Texture mapping

Bump mapping

Displacement mapping

task4

task5

空间内直线与三角形求交算法 Moller Trumbore

$$ \text{ray: } O + t\vec{D}\ \ , \vec{D} \text{ is unit vector, O is the origin point}\\ V_0, V_1, V_2\text{ is the three points of the trangle}\\ \text{Assume ray intersect with the triangle, and the intersection is P, use ray equation to represent P,} \\ P = O + t\vec{D}\\ \text{Also, we can use barycentric coordinates to represent P,}\\ P = (1-b_1-b_2)V_0 + b_1V_1 + b_2V_2\\ \text{Hence,}\ \ O + t\vec{D} = (1-b_1-b_2)V_0 + b_1V1 + b_2V_2\\ O - V_0 = b_1(V_1-V_0) + b2(V_2-V_0)-t\vec{D}\\ \vec{V_0O} = b_1\vec{V_0V_1} + b_2\vec{V_0V_2}-t\vec{D}\\ \text{The matrix form is},\\ \vec{V_0O} = \pmatrix{-\vec{D}\ \ \vec{V_0V_1}\ \ \vec{V_0V_2}}\pmatrix{t\b1\b2}\\ \text{Let }\vec{S} = \vec{V_0O},\ \vec{E_1} = \vec{V_0V_1},\ \vec{E_2} = \vec{V_0V_2},\\ \vec{S} = \pmatrix{-\vec{D}\ \ \vec{E_1}\ \ \vec{E_2}}\pmatrix{t\b1\b2}\\ \text{Use Clem's Law,}\\ t = \frac{det\pmatrix{\vec{S}\ \vec{E_1}\ \vec{E_2}}}{det\pmatrix{-\vec{D}\ \vec{E_1}\ \vec{E_2}}}\\ \text{Cause } det\pmatrix{-\vec{D}\ \vec{E_1}\ \vec{E_2}} = (\vec{S}\times\vec{E_1})\cdot\vec{E_2},\ \ det\pmatrix{-\vec{D}\ \vec{E_1}\ \vec{E_2}} = -(\vec{D}\times\vec{E_1})\cdot\vec{E_2} = (\vec{D}\times \vec{E_2})\cdot\vec{E_1}\\ t = \frac{(\vec{S}\times\vec{E_1})\cdot\vec{E_2}}{(\vec{D}\times \vec{E_2})\cdot\vec{E_1}}\\ \text{Let }\vec{S_2} = \vec{\vec{S}\times\vec{E_1}},\ \vec{S_1} = \vec{D}\times\vec{E_2},\\ t = \frac{\vec{S_2}\cdot\vec{E_2}}{\vec{S_1}\cdot\vec{E_1}}\\ \text{Ultimately,}\\ \pmatrix{t\b_1\b_2} = \frac{1}{\vec{S_1}\cdot\vec{E_1}}\pmatrix{\vec{S_2}\cdot\vec{E_2}\\ \vec{S_1}\cdot\vec{S}\\ \vec{S_2}\cdot\vec{D}}\\ \text{where, } \vec{S} = \vec{V_0O},\ \vec{E_1} = \vec{V_0V_1}, \vec{E_2} = \vec{V_0V_2},\ \vec{S_2} = \vec{S}\times\vec{E_1},\ \vec{S_1} = \vec{D}\times\vec{E_2}. $$

Clip Space, NDC(Normalizeds Device Coordinates) Space, Screen Space

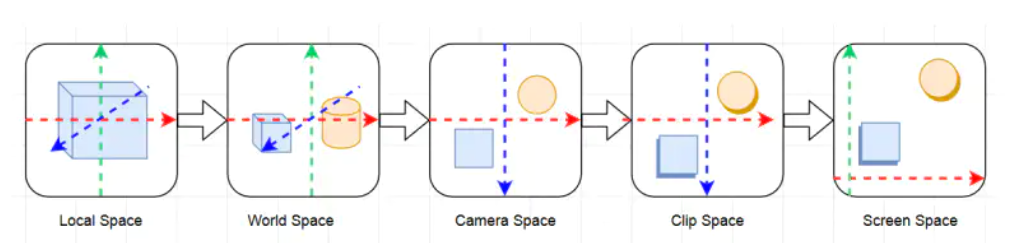
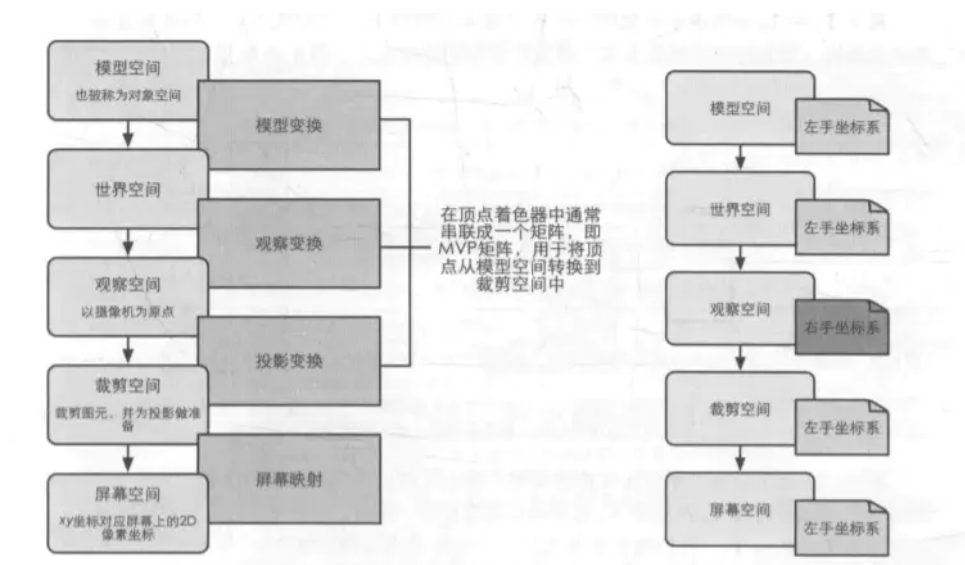
Model Space$\stackrel{model\ transformation}\longrightarrow$World Space$\stackrel{view\ transformation}\longrightarrow$View Space$\stackrel{projection\ transformation}\longrightarrow$Clip Space$\stackrel{screen\ mapping}\longrightarrow$Screen Space

task6

task7

spp = 1024

spp = 2048