Logistic Regression
This model can be seen as a generalization of the linear regression model by taking the hyperplane and shaping it differently with a non-linear function, in this case being a sigmoid function.
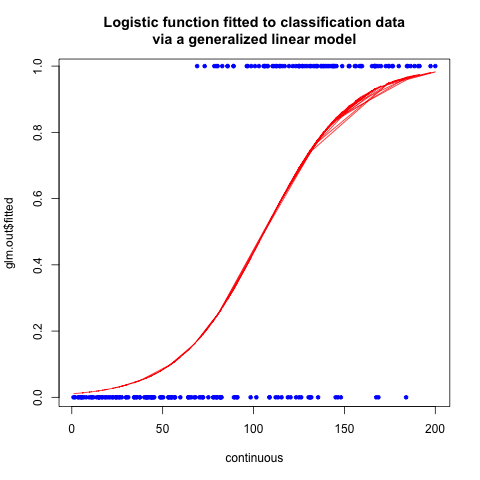
As the above image depicts, this model typically expects to predict variables that take values 0 or 1. It commonly expresses that either one event (0) or another (1) has happened experimentally, which can be seen as categorical values. Therefore, logistic regression is more commonly used as a binary classifier than an actual regressor.
Again, like the linear model, we want to predict the outcome of the observed phenomenon. Since the sigmoid function takes values between 0 and 1, it can be interpreted as the probability <math>P\equiv Y</math> of an event happening. In statistics, when talking about a Bernoulli Distriburion, we define the fraction <math>\frac{P}{1-P}</math> as the odds of an event happening which, as the formula indicates, expresses the proportion of the likelihood of an event happening over another (normally mutually exclusive). Additionally, its natural log <math>ln(\frac{P}{1-P})</math> is called the logit.
This can be seen a non-linear function <math>f(\cdot)</math> applied on top of the previously discussed linear model, in particular a sigmoid function:
<math>\widehat{P} \equiv \widehat{Y} = f(X*\beta)=\frac{1}{1+e^{-X*\beta}} \Rightarrow ln(\frac{\widehat{P}}{1-\widehat{P}})=X*\beta</math>
The beauty of the above non-linear transformation is that, defining the logit <math>L</math> as:
<math>L \equiv ln(\frac{P}{1-P})</math>
The problem then transforms into:
<math>\widehat{L} = X*\beta</math>
Which looks like and can be solved as a linear regressor.
Therefore, the learning will be performed as a linear model, using T instead of Y:
<math>\beta = (X^TX)^{-1}X^TL</math>
In addition to the advantages described for the linear regressor, a logistic regressor can be used as a binary classifier, instead of a mere regressor.
We can apply the same extension as in the linear regressor.
In this case, if the same trick <math>\widetilde{X}=(1|X)</math> is performed, the model will adjust for shifting the sigmoid function right and left.
The sigmoid non-linearity can better describe some data mining problems, but although the hyperplane has now acquired a more fancy shape, the data is still expected to fall close to its surface. Data mining problems that fall far from this assumption will thus not be well described with the Logistic Model.